This category of material includes notes introducing R and providing some vignettes on its use that may be of interest to economists. Additional material is available in PDF form in the downloads. These scripts are provided with no support or warranty or guarantee as to their general or specific usability. Most recent articles are shown first
Indexed Access To Cansim Series In R
In this example, we will use the cansim package to access gender-specific data by vector from Statistics Canada’s NDM using the cansim package from Mountain Math.
Packages USED
The key package used in this vignette is the cansim package which accesses vectors, in this case, from the NDM database of Statistics Canada. Key packages include
- Dplyr/tidyverse – for processing the tibble
- ggplot2 – part of tidyverse for plotting the results
- cansim – package to access data using the NDM api.[1]
Project Outline
NDM product tables (aka CANSIM) can be retrieved with a wealth of classification or META data as well as the coordinate. The latter provides a superlative index into the structure of the table. One of the challenges with many tables is that they contain more information than required for a particular project in terms of both data observations and detail of vectors. The retrieval can be simplified by just retrieving vectors for specific observations. However, the challenge is to easily and flexibly select vectors. The coordinate identifier and associated meta data can be used to select series. This allows the creation of scripts in which the series can be appropriately organized by concept (gender, province etc) and for the time range required. This can result in a substantial increment in speed and more importantly provide a structured organization to the retrieval. The latter facilitates the use of the more power features of tidyverse.
This note documents two scripts:
1)one-time retrieval of full table and creation of an index file which is simply the last observation of the table.
2)Retrieve required v numbers and observations to plot the change in employment rates since a particular period of time.
Script 2 is much more efficient to run and re-run because only a portion of the time series and observations are retrieved.
In corporate environments, it may be necessary to use a proxy setting. This is documented in the citation for the cansim package above.
All scripts will be available in the download section. https://www.jacobsonconsulting.com/index.php/downloads-2/indexed-access-to-ndm-series-in-r/download
Developing the Index File
This script is quite simple. The table is retrieved and saved as an RDS file (not really needed in this case). After retrieval, the table is filtered for the last observation only and saved as an RDS file with an appropriate file name.
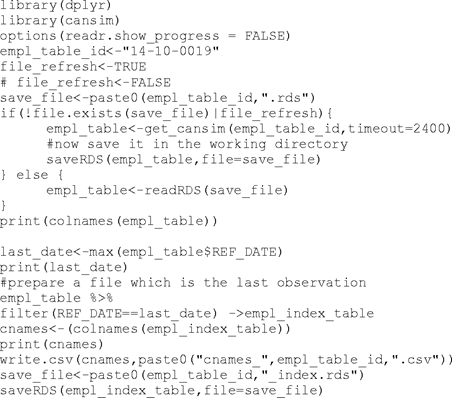
The original table from the retrieval need not be saved. The index file includes all the columns such as value and date for reference purposes. A csv file of the column names is saved for documentation.
Employment Rates
The base table used for this analysis contains significant detail by age and employment type. Because we want to show employment rates for full- and part-time workers, we must calculate employment rates on the fly as the ratio of employment to source population. The first script segment defines the packages used and retrieves the index table using readRDS, the reverse of the command used to save it above.

The next segment unpacks the index table to separate the coordinate into addressable single indexes, Columns that are not required are also dropped.

The columns of the coordinate are renamed to useful variable names. These will be used to select the vectors required. This is much easier than trying to select by the text variables in the basic table. The latter are matched to the coordinate codes to provide a mapping for use in selecting text entries and other documentation. Because we do not want to show all levels of education attainment, the education table is extended to include an aggregation variable, “edtype”. This will be used to collapse employment and population.
The values used to select the series are determined by examining the tables created above.

The code segment above defines some key parameters and selects and aggregates the source. Population by summarizing over the “edtype” variable. Note that the variables from the index table are joined with the data required from NDM so that the full attribute set is available.
The next set of code starts the main loop. Looping is over labour force type (full- and part-time), gender and time.

The next set of code prepares the basic analytical rates by joining the tibble retrieved above with the population tibble after appropriate aggregation. Note that the population tibble is joined using all the relevant classification variables. We are calculating year over year growth rates but also growth rates from February 2020. The code was originally set up to process the current and preceding months.

The next segment calculates shares of change and employment for analytical purposes.

Charts for four displays are planned. After setting up the parameters, the basic data is adjusted to select the date to plot, the gender and to copy the variable to plot to a specific variable in the data set that can be referenced in the ggplot2 package. The “.data” element is referred to as a pronoun in the tidyverse programming documentation. The reference is https://dplyr.tidyverse.org/articles/programming.html.

The next code segment uses plot_data_2 in ggplot with the parameters defined above to characterize the chart.

Note that the plot_value variable is used to position the text label above the actual bar.
The final code segment saves each plot as a separate png and builds up a list of pngs which is saved for subsequent processing into a PDF or other report.

[1] https://www.rdocumentation.org/packages/cansim
1) one-time retrieval of full table and creation of an index file which is simply the last observation of the table.
2) Retrieve required v numbers and observations to plot the change in employment rates since a particular period of time.
Gender-Based Wage Rate Charts With Cansim Using R
In this example, we will use the cansim package to access gender-specific data by vector from Statistics Canada’s NDM using the cansim package from Mountain Math.
Packages USED
The key package used in this vignette is the cansim package which accesses vectors, in this case, from the NDM database of Statistics Canada. Key packages include
- dplyr – for processing the tibble
- ggplot2 – part of tidyverse for plotting the results
- cansim – package to access data using the NDM api.[1]
The script uses a pre-defined list of vectors to produce charts by gender for the occupations included in the vector list. The focus in this example is on full-time wages by gender for two management occupations.
In corporate environments, it may be necessary to use a proxy setting. This is documented in the citation for the cansim package above.
Retrieve the data
The initial stage is to retrieve the vectors. The script below assumes that the user’s R profile defines the appropriate working folder or else this should be defined in an initial use of the function setwd. The initial code processes a list of vectors delimited only with carriage returns such as would be obtained from a paste operation from some file. The character vector is split into a regular character vector with one entry per V number using strsplit. The “n” symbol is “escaped’ by a backslash so as to be treated as a carriage return. This process just saves enclosing each vnumber in quotes.
-
library(dplyr) -
library(cansim) -
library(tidyr) -
library(lubridate) -
library(stringr) -
library(ggrepel) -
library(ggplot2) -
#series list (management, full time) -
#list separate by carriage returns (i.e. copied from Excel) -
base_list <- " -
v103555126 -
v103555130 -
v103555138 -
v103555142 -
v103558798 -
v103558802 -
v103558810 -
v103558814 -
" -
raw_list <- strsplit(base_list, "\n") -
vbl_list <- unlist(raw_list) -
vbl_list <- vbl_list[vbl_list != ""] -
#now do the retrieval -
#analyze meta data -
meta1 <- get_cansim_vector_info(vbl_list) -
cube_meta <- get_cansim_cube_metadata(unique(meta1$table)) -
common_meta <- -
left_join(meta1, cube_meta, by = c("table" = "productId")) %>% distinct() %>% -
select(VECTOR, table, title_en, cubeTitleEn, cubeEndDate) -
print(as.data.frame(common_meta)) -
#retrieve data -
cansim_vbls <- -
get_cansim_vector(vbl_list, start_time = as.Date("1995-01-01")) -
print(colnames(cansim_vbls))
In the code above, the vector list (vbl_list) is used to first get the meta data for the vectors. Unique table identifiers are used to retrieve the meta data for the tables involved. In this example, the vnumbers are all in one table. The print statement would show the following information.

The data are retrieved using the get_cansim_vector function. A start date must be supplied.
The next code parses the title_en variable in common_meta which is the description for each vector. This is simply the text attributes of the vector concatenated with a semi-colon between each one.
#now parse the title_en for key fields specific to the variables chosen#title en substrings are in the order specific to the NDM tablestitle1 <- str_split_fixed(common_meta$title_en, fixed(";"), n = Inf)#need to supply column namestitle1_names <- paste0("col", 1:ncol(title1))colnames(title1) <- title1_namestitle_tbl <- tbl_df(title1) %>%rename( region = 1, wage_type = 2, employee_type = 3, occupation = 4, gender = 5, age_range = 6)title_table <- bind_cols(VECTOR = common_meta$VECTOR, title_tbl)print(title_table)class_vbls <- colnames(title_table)The vector class_vbls contains the column names provided in the rename statement above. This will be used below in a variable select. The next code uses dplyr to join this classification information with the VECTOR identifier to the cansim_vbls tibble retrieved above.
cansim_vbls %>%left_join(title_table, by = "VECTOR") %>%mutate(date = as.Date(REF_DATE)) %>%select(VECTOR, REF_DATE, date, VALUE, one_of(class_vbls[-1])) -> working_data#the vector in class variables is droppedhead(working_data)Doing the plots
In the next set of code, lists are prepared for the various classification variables which are used to select the data to be plotted. We use a string to select the wage type because we want to include both average and median wage rates.
#lets do separate plots for each occupationoccupation_list <- unique(title_table$occupation)wage_list <- unique(title_table$wage_type)print(wage_list)type_of_wage <- "weekly"employee_type_list <- unique(title_table$employee_type)type_of_employee <- employee_type_list[1]age_list <- unique(title_table$age_range)age_group <- age_list[1]plot_list <- character()plot_counter <- 0The occupation list is used to define the structure of the “for” loop to control the occupations to be plotted. More occupations could be included in the vector list. The first stage is to build the plot_data tibble by filtering on all of the classification variables that can vary. If multiple geographies are included in the vector list, then the region classification must be included in the filter.
for (occupation_counter in seq_along(occupation_list)) {this_occupation <- occupation_list[occupation_counter]#we filter the working data for the attributes that we are not using in the chart#we are selecting all weekly wage typesworking_data %>% filter( occupation == this_occupation, str_detect(wage_type, "weekly"), employee_type == type_of_employee, age_range == age_group ) -> plot_dataThe next piece of code prepares various text strings which are also used in the plot for documentation including the range of the data. Then, a last_values tibble is constructed containing the data for only the first and last data points. This will be used for plot labelling.
vector_list <- paste(unique(plot_data$VECTOR), collapse = ",")#get first and last datelast_date <- substr(max(plot_data$date), 1, 4)first_date <- substr(min(plot_data$date), 1, 4)#calculate a tibble for the values of the first and last datapoints# for labeling the plotplot_data %>% group_by(occupation, wage_type, employee_type, age_range, gender) %>% arrange(date) %>% slice(c(1, n())) -> last_valuesNow the actual plot is started. This is relatively standard with color attributes being assigned to gender and the linetype attribute used to distinguish average and median wages in this example. The geom_label_repel function is used to apply the label layer because it positions the labels in more aesthetically pleasing places on the chart.
wage_plot1 <- ggplot(plot_data, aes( x = date, y = VALUE, colour = gender, linetype = wage_type )) + labs( title = this_occupation, subtitle = paste( type_of_employee, "\n", "Annual Average of Weekly wages", first_date, "-", last_date ), y = "$", x = NULL, caption = paste("Statcan:", vector_list, "JCI ", Sys.Date()) ) + theme(legend.title = element_blank()) + geom_line() + geom_label_repel(data = last_values, aes(label = round(VALUE, 0), colour = gender))print(wage_plot1)ggsave( wage_plot1, file = paste0("wage_", type_of_wage, "_", this_occupation, ".png"), width = 12, height = 7.5)plot_counter <- plot_counter + 1unique_plot_name <- paste0("plot_", plot_counter)assign(unique_plot_name, wage_plot1)plot_list <- c(plot_list, unique_plot_name)}Note that the vector list is included in the plot caption. The last portion of the loop creates a unique name for each plot and builds up a text list of plot names for subsequent processing. The final piece of code simply groups the plots into a single two-plot png.
library(gridExtra)these_plots <- mget(plot_list)stacked_plots <- marrangeGrob(these_plots, nrow = 2, ncol = 1, top = NULL)ggsave(stacked_plots, file = "wage_rate_plots.png", width = 12, height = 15)The resulting two-plot png is shown below.

Musings on Seasonal Adjustment and The Labour Force Survey
Introduction
This note outlines some thoughts about seasonal adjustment. Examples from R will be supplied. The specific context of the material is in relation to the Labour Force Survey but much of the remarks are relevant to the analysis of other data.[1][2] Where possible, references have been chosen which are freely available on the web.
What is Seasonal Adjustment?
Many timeseries with a sub-annual periodicity may exhibit regular seasonal patterns each year. These seasonal patterns will arise because of a combination of factors related to calendar effects (school years, holidays, etc.), weather (climate), timing decisions (dividends), etc. Granger emphasizes that timeseries may have different causes of seasonality and thus may show different seasonal patterns.(Granger 1978)
These patterns often obscure the underlying trends in the data. The seasonal adjustment process uses mathematical techniques to decompose the initial raw timeseries into three timeseries components:
- Seasonal
- Trend-Cycle
- Residual
Combined, the three components, processes underlying the original series, are equivalent to the original series. Since it is a mathematical transformation, seasonal decomposition is a statistical estimate. We cannot separately measure the components. Multiplicative models may be appropriate to cases in which the seasonal pattern is proportionate to the level of the series. Additive models may otherwise suffice. This is discussed in Chapter 6 of Hyndman and Athanasopoulos (HA).(Hyndman and Athanasopoulos 2018)
In the context of the Labour Force Survey (LFS), Statistics Canada directly measures each month of data with a household survey instrument. Each individual unweighted observation represents pure measured data. Population-level estimates are developed by applying population weights to each observation to get appropriately scaled values. This is more of a statistical process since the population weights are subject to error and revision. Except when the population weights are revised, with the availability of a new census, the data remain unchanged. The underlying unweighted observation is not revised.(Government of Canada 2018)
The basic seasonal adjustment estimation process is to filter out the seasonal and trend components using some statistical filter such as centered moving averages. The goal is to identify patterns and remove data that are explained by seasonality. The Australian Bureau of Statistics (ABS) has an excellent summary of the basic process involved in the X11 analysis. They explain the general steps on their web site.(Australian Bureau of Statistics n.d.) The basic approach involves three steps:
- Estimate the trend by a moving average
- Remove the trend leaving the seasonal and irregular components
- Estimate the seasonal component using moving averages to smooth out the irregulars.
The process is iterative because the trend cannot really be identified until the seasonal and irregular residual components have been estimated. The ABS site has a step by step outline of the process.
Eurostat publishes a handbook which covers the field very well with chapters by major practitioners.(Mazzi and Ladiray 2018) The chapter on timeseries components reviews the general characteristics of the components and the type of models, generally deterministic or stochastic, used to estimate the trends.(Dagum and Mazzi 2018) In this chapter, Dagum and Mazzi discuss the issues of modelling moveable holidays, such as Easter, and trading day variations.
One issue raised is the treatment of outliers. Special estimate may be required for significant strikes or weather events. The example of the big ice storm in Canada is used as what are termed as redistributive outliers which may shift the pattern of seasonality. This may require special modelling.
Some Tools
The X11 approach was developed at the Bureau of the Census in the US and substantially refined and enhanced at Statistics Canada. Modern seasonal adjustment practice owes a great deal to our statistics agency. At StatCan, the process was enhanced to use ARIMA modelling to back- and forward-cast the series because otherwise the centered filters have difficulties with endpoints because there are not enough observations for the full range of weights.
ARIMA stands for Auto Regressive Integrated Moving Average. It is a technique for forecasting time series based on moving averages. Chapter 8 in H-A introduces the key concepts and discusses their use in forecasting.
The SEATS “Seasonal Extraction in ARIMA Time Series” decomposition method has been incorporated in the latest version of the X series (X13Arima-SEATS) by the Bureau of the Census in the US.(US Census Bureau n.d.) The SEATS process only works on quarterly and monthly data. The author of the R seasonal package, Christoph Sax, which interfaces to the Census software, has developed an excellent web site which facilitates the online use of the software and experimentation with parameters.(Sax n.d.) It is possible to upload series and directly process them on this site. This site also facilitates the testing of specific modelling assumptions for trading days and outliers. The latter capability is a key attribute of the X-family of seasonal adjustment procedures. In his R package, Sax facilitates the use of the full modeling facilities of X13-SEATS/X-11. He has also implemented a view function which emulates his web site.[3]
Another approach (STL) uses locally-weighted regressions (LOESS) as smoothers to estimate the components.(Cleveland et al. 1990) The STL algorithm, which is included in the base version of R, has the advantage of being useful for daily, weekly and any other timeseries with “regular” periodicity that can be fit into a TS object in R.[4]
Both X-11 (Henderson) and STL (Loess) use smoothing processes or filters to identify the trend-cycle component. Dagum reviews the use of these tools for local trend-cycle estimation.(Dagum 2018) Her analytical charts indicate a strong similarity of the results for the Henderson and Loess filters.
Examples of these decomposition procedures will be shown later in this note. However, there are many other similar techniques which will not be evaluated for this note.
Usage Considerations
The estimation of the components of a seasonal timeseries will change with each new data point. This implies that history gets revised. The practice at Statistics Canada is to revise only the immediate past observation until the end of the year. This is equivalent to leaving the factors used to extract the seasonal portion unchanged. With the beginning of the new year, the seasonal factors are revised back by estimating the full data series. With the LFS, this is introduced into the public dataset close to the release of the January data. This year, StatCan released the revisions at the beginning of February 2018. The chart below shows the impact of the revisions on month-to-month changes in the aggregate level of employment.

Figure 1 Monthly Season Revisions 2019-02-01
One of the challenges with processing data through seasonal adjustment or other filtering algorithms is the requirement to keep consistency between various levels of aggregation. The LFS has data by province, industry and demographic characteristic so consistency is a challenge. In the LFS case, it is handled by “raking” the series in each direction to maintain consistency of aggregation.(Fortier and Gellatly n.d.)
Some Examples of Seasonal Adjustment
In this section, we will just review some mechanical examples of seasonal adjustment. Various R packages will be used. These will be outlined in the appendix which reviews the example script. In all cases, the forecast package, developed by Rob Hyndman, is loaded because it provides useful support to the management of ts objects (regular-periodicity time series) in R.(“Forecast Package | R Documentation” n.d.) There is an excellent introduction to the seasonal decomposition techniques in Chapter 6 of the Hyndman - Athanasopoulos book.(Hyndman and Athanasopoulos 2018) At the start of the chapter, the book provides a brief but useful summary of classical decomposition techniques using moving average filters. These techniques have been replaced with the more modern seasonal adjustment packages.
In these examples, the same series, monthly employment for 15+, is used. Outlier detection has been left enabled for the X-family examples and the robust method has been used for STL.
X11
The Census software supports both x11ARIMA and the SEATS approach. The seasonal package is used to prepare the interface information and extract results for both.(Sax and Eddelbuettel 2018) The initial example is just for the X11 variant.
The results from the analysis are shown below:
x11 ResultsCall:seas(x = stc_raw, x11 = "")Coefficients: Estimate Std. Error z value Pr(>|z|) LS2008.Nov -146.75083 34.92917 -4.201 2.65e-05 ***LS2009.Jan -184.01995 34.92948 -5.268 1.38e-07 ***MA-Nonseasonal-01 0.07721 0.05937 1.300 0.193 MA-Seasonal-12 0.61281 0.04961 12.352 < 2e-16 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1X11 adj. ARIMA: (0 1 1)(0 1 1) Obs.: 288 Transform: noneAICc: 2811, BIC: 2829 QS (no seasonality in final): 0Box-Ljung (no autocorr.): 26.5 Shapiro (normality): 0.9962Figure 2 X11 Summary Results
The analysis identifies Nov 2008 and January 2009 as significant, which is the start of the Great Recession. The seasonally adjusted series was shown to have no residual seasonality by the tests applied. The next chart shows the seasonal components extracted from the analysis. Note that scale of each component chart is independent. In reviewing the chart, note that the algorithm identified the break in trend and that the unexplained residuals are relatively small. The seasonal estimates do not increase in size over time.

Figure 3 X11 Decomposition
SEATS Example
Extending the analysis to the SEATS procedure produces similar results.
X13 ResultsCall:seas(x = stc_raw)Coefficients: Estimate Std. Error z value Pr(>|z|) LS2008.Nov -146.75083 34.92917 -4.201 2.65e-05 ***LS2009.Jan -184.01995 34.92948 -5.268 1.38e-07 ***MA-Nonseasonal-01 0.07721 0.05937 1.300 0.193 MA-Seasonal-12 0.61281 0.04961 12.352 < 2e-16 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1SEATS adj. ARIMA: (0 1 1)(0 1 1) Obs.: 288 Transform: noneAICc: 2811, BIC: 2829 QS (no seasonality in final): 0Box-Ljung (no autocorr.): 26.5 Shapiro (normality): 0.9962Messages generated by X-13:Warnings:- At least one visually significant trading day peak has beenfound in one or more of the estimated spectra.Figure 4 X13-SEATS Summary Results
The component chart below shows similar results to the X-11 variant

Figure 5 X13SEAT Components
The residual variation is slightly smaller probably reflecting the type of filters applied. However, the differences in scales should be noted.
STL Example
The final example uses the mstl procedure in the forecast package to iterate the stl procedure automatically to tighten the estimation on the seasonal patterns. The output is relatively simple, showing the distribution of the components.
stl Results Data Trend Seasonal12 Remainder Min. :12894 Min. :13242 Min. :-364.936 Min. :-160.7521st Qu.:14847 1st Qu.:14870 1st Qu.:-239.970 1st Qu.: -15.653Median :16484 Median :16575 Median : 18.923 Median : 0.802Mean :16195 Mean :16194 Mean : -0.175 Mean : 1.2593rd Qu.:17542 3rd Qu.:17572 3rd Qu.: 202.352 3rd Qu.: 17.801Max. :18979 Max. :18730 Max. : 376.106 Max. : 249.917Figure 6 MSTL Summary
Reviewing the component charts below indicates that the STL algorithm produces a similar trend estimate with a noticeable break but not as sharp. H-A suggest that STL has several advantages:
STL has several advantages over the classical, SEATS and X11 decomposition methods:
- Unlike SEATS and X11, STL will handle any type of seasonality, not only monthly and quarterly data.
- The seasonal component is allowed to change over time, and the rate of change can be controlled by the user.
- The smoothness of the trend-cycle can also be controlled by the user.
- It can be robust to outliers (i.e., the user can specify a robust decomposition), so that occasional unusual observations will not affect the estimates of the trend-cycle and seasonal components. They will, however, affect the remainder component.
On the other hand, STL has some disadvantages. In particular, it does not handle trading day or calendar variation automatically, and it only provides facilities for additive decompositions.[5]
Generally, the residuals are larger for the test case than the X-family examples shown previously. The break in the trend is less extreme than that found by the X-family examples.

Figure 7 STL Decomposition
As in the other example, the analysis was run using the simplest automatic approach. However, a robust estimation procedure was used which moves the effect of outliers to the remainder rather than letting them affect the other components.
The next two charts compare the track of the examples over the full available sample period as well as in the recent period. Note that all the algorithms track the StatCan estimate well and produce a similar break for the Great Recession. However, the trend-cycle estimate from the STL approach has a less sharp break in the trend but wider swings in the irregular remainder at the break point.

Figure 8 Example Comparison over Full Sample
The next graph tightens the focus to recent observations and changes the scale. As would be expected because of the similarity of the approaches, the X-11 and the SEATS variant, used in automatic mode, track the StatCan X-12 estimate best.

Figure 9 Seasonal Adjustment Comparison 2016 forward
Comparison charts of the irregular remainder are shown below. All forms of seasonal adjustment are constrained to the standard identity that the sum of the three components is identical to the original raw series. As noted earlier, the STL procedure used a robust estimation approach which tends to move the impact of outliers to the irregular remainder rather than moving them to the trend estimate.

Figure 10 Comparison of Seasonal Adjustment Residuals
The other components are shown in Appendix A. The plot of the trend-cycle measure has been done with 3 panels and as a common chart in that appendix. The charts show that the STL algorithm has created a smoother trend and allocated the outliers to the Residuals component in comparison to the X-family estimates.
The next table shows the basic statistics for the components for each of the seasonal adjustment methods.
|
Statistic |
N |
Mean |
St. Dev. |
Min |
Pctl(25) |
Pctl(75) |
Max |
|
stl_seasonal |
288 |
-0.175 |
242.486 |
-364.936 |
-239.970 |
202.352 |
376.106 |
|
x11_seasonal |
288 |
-0.114 |
240.267 |
-368.705 |
-245.108 |
198.570 |
389.129 |
|
x13_seasonal |
288 |
-0.119 |
240.648 |
-376.648 |
-250.298 |
187.044 |
390.193 |
|
stl_trendcycle |
288 |
16,193.750 |
1,607.167 |
13,241.890 |
14,869.920 |
17,572.030 |
18,729.710 |
|
x11_trendcycle |
288 |
16,194.330 |
1,610.948 |
13,257.400 |
14,891.950 |
17,585.100 |
18,808.450 |
|
x13_trendcycle |
288 |
16,194.950 |
1,610.782 |
13,251.060 |
14,892.060 |
17,582.950 |
18,803.610 |
|
stl_irregular |
288 |
1.259 |
44.890 |
-160.752 |
-15.653 |
17.801 |
249.917 |
|
x11_irregular |
288 |
0.616 |
17.404 |
-58.303 |
-8.026 |
8.947 |
74.379 |
|
x13_irregular |
288 |
-0.000 |
10.986 |
-29.557 |
-7.095 |
7.522 |
36.113 |
Figure 11 Descriptive Statistics for Components
The next figure shows the descriptive statistics for the full sample period for the seasonally adjusted data.
|
Statistic |
N |
Mean |
St. Dev. |
Min |
Pctl(25) |
Pctl(75) |
Max |
|
empl_stl_sa |
288 |
16,195.000 |
1,611.077 |
13,228.190 |
14,883.320 |
17,586.900 |
18,864.350 |
|
empl_x11_sa |
288 |
16,194.940 |
1,610.988 |
13,240.000 |
14,892.170 |
17,585.160 |
18,818.820 |
|
empl_x13_sa |
288 |
16,194.950 |
1,610.884 |
13,245.640 |
14,890.680 |
17,581.590 |
18,803.690 |
|
stc_sa |
288 |
16,196.400 |
1,611.340 |
13,262.300 |
14,887.500 |
17,605.950 |
18,808.400 |
Figure 12 Descriptive Statistics for Seasonally Adjusted Series
The statistics are relatively standard for all the estimates. To the extent that the estimation process shifts variations between the trend-cycle and irregular components, there is no loss of information in the final seasonally adjusted series. However, if the filtering process shifts information to the estimated seasonal patterns inappropriately, information may be lost. That is the challenge with filtering algorithms. It should be noted that the current stc_sa estimates were retrieved prior to the update of the seasonal factors. Both the X variants show the most modest irregulars with X-13 having the shallowest ones. This means that more variation has been moved to the trend component than in the stl alternative.
A Trend is a Trend is a Trend
The heading is the start of a famous poem attributed to Sir Alex Cairncross:
A trend is a trend is a trend. But the question is, will it bend? Will it alter its course through some unforeseen force and come to a premature end?[6]
One of the main reasons for seasonally adjusting a series is to focus on the trend. If the decompositions are available, the trend, known as the trend-cycle, can be easily extracted. However, if only the seasonally-adjusted final result is available, some other approach is required. StatCan has documented a procedure to extract a trend from its seasonally-adjusted series using (for monthly data), a centered 13-period filter with exponentially declining weights on each side.(Government of Canada et al. 2015) StatCan supplies it for a few key series. However, the technique is applicable to other series. The chart below shows the recent estimate of the seasonally-adjusted LFS15+ employment and the associated trend-cycle estimate.

Figure 13 LFS15+ Employment and Trend-Cycle estimate
The latter part of the trend is shown as a dotted line to indicate that only a portion of the filter was used. The final data point is filtered only with half of the filter. This trend-cycle estimate should likely be used for planning purposes rather than direct analysis of the more volatile monthly series.
Estimates Have a Distribution
The final chart in this note pairs two charts showing the monthly and year-over-year change in the LFS15+ series. StatCan provides estimates of the standard error for these measures of change. These are shown as error bars at the 68% level. These standard error estimates are discussed in the notes at the end of the LFS Daily release. Since the survey samples are assumed to be normally distributed, the point estimate is assumed to be the most likely result. However, one should always be aware the “true” number might be even outside the line shown but with a very low probability. The 95% confidence interval error bar would be almost twice as long. Thus, caution should be exercised in the interpretation of recent changes. The value scales are much different in the two charts. It should be noted that the error bars for the year-over-year change are much smaller in proportion to the change. This suggests some usefulness in that form of comparison.

Conclusions
The purpose of this note is to outline how seasonal adjustment works and to provide an example using Canadian data of several processes which are available in R. An appendix reviews the R code used to produce the examples. Results are broadly similar, but the modern X-family examples show why these programs are used for monthly and quarterly data by the major statistical authorities. The important points to consider are:
- Additional data changes the estimation process resulting in differences in the estimated decomposition between seasonal, trend-cycle and irregular components.
- This can result in changes in patterns of the period-to-period seasonally adjusted observations but would not likely affect the estimate of the general trend.
- Seasonal adjustment techniques were developed to facilitate a focus on longer term trends that were obscured by seasonality. The mathematical filters involved may obscure or modify the period-to-period changes in such a way as to modify the information content. Care should always be taken with short-term analysis.
- Specific consideration of outliers related to major weather events or significant strikes may be required but automatic procedures may suffice.
- The trend-cycle component is a valuable indicator of the direction of change in the target series.
Bibliography
Australian Bureau of Statistics. n.d. “Australian Bureau of Statistics Time Series Analysis: Seasonal Adjustment Methods.” Accessed January 22, 2019. http://www.abs.gov.au/websitedbs/d3310114.nsf/4a256353001af3ed4b2562bb00121564/c890aa8e65957397ca256ce10018c9d8!OpenDocument.
Cleveland, Robert B., William S. Cleveland, Jean E. McRae, and Irma Terpenning. 1990. “STL: A Seasonal-Trend Decomposition.” Journal of Official Statistics 6 (1): 3–73.
Dagum, Estela Bee. 2018. “14 - Trend-Cycle Estimation.” In Handbook on Seasonal Adjustment, 2018th ed. Luxembourg: European Union. https://ec.europa.eu/eurostat/documents/3859598/8939616/KS-GQ-18-001-EN-N.pdf/7c4d120a-4b8a-441b-aefd-6afe81a7cf59.
Dagum, Estela Bee, and Gian Luigi Mazzi. 2018. “3 - Time Series Components.” In Handbook on Seasonal Adjustment, 2018th ed. Luxembourg: European Union. https://ec.europa.eu/eurostat/documents/3859598/8939616/KS-GQ-18-001-EN-N.pdf/7c4d120a-4b8a-441b-aefd-6afe81a7cf59.
Fortier, Suzy, and Guy Gellatly. n.d. “Seasonally Adjusted Data - Frequently Asked Questions.” Accessed January 22, 2019. https://www150.statcan.gc.ca/n1/dai-quo/btd-add/btd-add-eng.htm.
Government of Canada, Statistics Canada. 2018. “Guide to the Labour Force Survey, 2018.” September 7, 2018. https://www150.statcan.gc.ca/n1/pub/71-543-g/71-543-g2018001-eng.htm.
Government of Canada, Statistics Canada, Suzy Fortier, Steve Matthews, and Guy Gellatly. 2015. “Trend-Cycle Estimates – Frequently Asked Questions.” August 19, 2015. https://www.statcan.gc.ca/eng/dai/btd/tce-faq.
Granger, Clive WJ. 1978. “Seasonality: Causation, Interpretation, and Implications.” In Seasonal Analysis of Economic Time Series, 33–56. NBER.
Hyndman, Rob J., and George Athanasopoulos. 2018. Forecasting: Principles and Practice. OTexts.
Mazzi, Gian Luigi, and Dominique Ladiray. 2018. Handbook on Seasonal Adjustment. 2018th ed. Luxembourg: European Union. https://ec.europa.eu/eurostat/documents/3859598/8939616/KS-GQ-18-001-EN-N.pdf/7c4d120a-4b8a-441b-aefd-6afe81a7cf59.
Sax, Christoph. n.d. “Seasonal: R Interface to X-13ARIMA-SEATS.” Accessed January 23, 2019. http://www.seasonal.website/.
Sax, Christoph, and Dirk Eddelbuettel. 2018. “Seasonal Adjustment by X-13ARIMA-SEATS in R.” Journal of Statistical Software 87 (11): 1–17.
US Census Bureau, Brian C. Monsell. n.d. “US Census Bureau - X-13ARIMA-SEATS Seasonal Adjustment Program - Home Page.” Accessed January 23, 2019. https://www.census.gov/srd/www/x13as/.
Appendix A – Additional Charts



Appendix B – R Code for the Examples
R - Examples - Code
This section reviews the code used to produce the examples in the preceding sections of the report. As well as base R, key packages include:
- dplyr – data frame/tibble manipulation
- cansim – retrieving variables from StatCan NDM (a.k.a. CANSIM)
- tidyyr – a tidyverse component to manipulate data frames and tibbles to and from tidy data structures
- ggplot2 – tidyverse graphics package
- lubridate – tidyverse package to manipulate dates
- tsbox – a package to work with timeseries objects
- forecast – useful timeseries tools including seasonal adjustment
- seasonal – x11/x13 seasonal adjustment
The use of “ts” objects throughout the code is needed to fit the requirements for “regular” periodicity objects. The tsbox package has translation functions to move from other data structures such as tibbles to ts objects. An alternative strategy is to manipulate the time data using packages such as xts/zoo and only convert to “ts” when doing seasonal adjustment. The autoplot extension in the forecast packages supports “ts” objects.
Much of the code is adequately commented. The first stage after initial package loads via the library function is to define a list of series and to retrieve them. The cansim package retrieves the series in vector order (i.e. sorted) into a tibble which is translated into a ts data frame using the ts_ts function from tsbox. If the position in the request list is critical, the retrieved data frame must be reordered. This is good standard practice as is the saveRDS function which is used to save a copy of the data with date.
library(dplyr)library(cansim)library(tsbox)library(tidyr)library(lubridate)library(ggplot2)library(forecast)#In this vignette, we are working with ts objects to suit the conventions of seasonal adjustmentcanada_lfs_vbls<-c("v2062811","v100304302","v101884904", "v101884905","v101884906","v2064890")#analyze meta datameta1<-get_cansim_vector_info(canada_lfs_vbls)cube_meta<-get_cansim_cube_metadata(unique(meta1$table))common_meta<-left_join(meta1,cube_meta,by=c("table"="productId")) %>%distinct()%>%select(VECTOR,table,title_en,cubeTitleEn,cubeEndDate)print(as.data.frame(common_meta))#now retrieve the datacanada_lfs_ts <- get_cansim_vector(canada_lfs_vbls,start_time=as.Date("1995-01-01")) %>%mutate(Date=as.Date(paste0(REF_DATE,"-01")))%>%select(Date,VECTOR,VALUE)%>%ts_ts()#order the series by the vector order in the requestcanada_lfs_ts<-canada_lfs_ts[,canada_lfs_vbls]#save the data vintagedsaveRDS(canada_lfs_ts,file=paste0("LFS_15_data_",Sys.Date(),".Rds"))The meta data for the series and corresponding NDM table are retrieved and displayed as well for documentation purposes.
The next section of code calculates the change variables needed for plotting the monthly change with standard errors.
last_year<-year(Sys.Date())-1window(canada_lfs_ts,last_year)print(colnames(canada_lfs_ts))print(data.frame(select(meta1,VECTOR,title_en)))#the first vector is lfs employment 15+#the fourth vector is the standard error of the month to month changelfs_change<-diff(canada_lfs_ts[,1],differences=1,lag=1)#the data have to be merged together to maintain the ts attributesdata1<-cbind(canada_lfs_ts[,1],lfs_change,canada_lfs_ts[,4])colnames(data1)<-c("LFS15+","DeltaLFS15+","SEDeltalfs15+")tail(data1,12)plot_data<-cbind(data1[,2],data1[,2]+.5*data1[,3],data1[,2]-.5*data1[,3])colnames(plot_data)<-c("DeltaLFS15","Upper","Lower")#making it into a wide data frame makes it easier to manage in ggplot because the date is accessible#subset method from forecast package is used to manage number of observations#that is easier than using the window commandnumb_obs<-nrow(plot_data)plot_data_tbl<-ts_tbl(subset(plot_data,start=numb_obs-23))#use spread from tidyr to make it wide so that upper and lower are easily#accessed#the ts_tbl function from the tsbox package has extracted the time variable from the#ts objects to make it a separate variableplot_data2<-spread(plot_data_tbl,id,value)The cbind command is used to merge the calculated variables into a data frame retaining the ts attributes. Because the forecast package is loaded, the subset function specifically recognizes “ts” objects. One challenge with “ts” objects is that the time concept is hidden as an attribute of the variables so particular procedures are required to manage the attributes. The ts_tbl, from the tsbox package, converts the ts data frame into a tall tibble with the variable names in the “id” variable. The ts_tbl also extracts the time concept into its own separate variable.
However, for the purposes of the plot, we need to access each variable (levels, upper and lower bounds) so the tibble is spread using the corresponding tidyyr function into a wide data structure.
#now calculate a date string for the captiondate_string<-paste0(substr(plot_data2$time[1],1,7),"/",substr(tail(plot_data2$time,1),1,7))head(plot_data2)#load the plot librarylibrary(ggplot2)plot1<-ggplot(plot_data2,aes(x=time,y=DeltaLFS15))+geom_point()+geom_pointrange(aes(ymin=Lower,ymax=Upper))+geom_line()+labs(title="Monthly Change in LFS 15+ Employment",y="Monthly Change (000)",x=NULL,subtitle="Seasonally Adjusted with Standard Error Bars",caption=paste(date_string," ","STATCAN:",paste(canada_lfs_vbls[c(1,4)],collapse=", "),"JCI"))ggsave(plot1,file="LFS15_monthly_change.png")Because the data had been reorganized into a wide tibble, the plot is relatively straight forward. The separate ymin and ymax variables provide the limits for the error bars produced by the pointrange geom overlay.
#now start a plot of the trend cycle and the total employment# review this link about trend cycle https://www.STATCAN.gc.ca/eng/dai/btd/tce-faq#we want to drop the last 12 observations from the trend cycle and add a third series which is just the tail of the trend cycle.dotted_period<-6data_chart2<-cbind(canada_lfs_ts[,1],head(canada_lfs_ts[,2],length(canada_lfs_ts[,2])-dotted_period),tail(canada_lfs_ts[,2],dotted_period))# tail(data_chart2,24)colnames(data_chart2)<-c("LFS15plus","Trend-Cycle","Trend Recent")numb_obs<-nrow(data_chart2)plot_data_trend<-subset(data_chart2,start=numb_obs-23)trend_tibble<-ts_tbl(plot_data_trend)date_string_trend<-paste0(substr(trend_tibble$time[1],1,7),"/",substr(tail(trend_tibble$time,1),1,7))#linetype and colur are managed in the alphabetic order of the series group in tibble.trend_plot<-ggplot(trend_tibble,aes(x=time,y=value,group=id,colour=id))+geom_line(aes(linetype=id))+scale_linetype_manual(values=c("solid","solid","dashed"))+theme(legend.position="bottom",legend.title=element_blank())+labs(title="Monthly LFS 15+ Employment",x=NULL,y="Monthly Level (000)",subtitle="Seasonally Adjusted",caption=paste(date_string_trend," ","STATCAN:",paste(canada_lfs_vbls[c(1,2)],collapse=", "),"JCI"))ggsave(trend_plot,file="LFS15_monthly_trend.png")Note the use of the caption to document the Vnumbers used in the chart. The line types are forced in this chart using the scale_linetype_manual function. The next set of code merges the two charts into one png file.
#gridExtra's grob management is useful#to group the graphic objects from the plots#the graphic objects are plot instructions not pngslibrary(gridExtra)plot_list<-mget(c("plot1","trend_plot"))two_plots<-marrangeGrob(plot_list,nrow=1,ncol=2,top=NULL)two_plot_name<-"lfs_se_trend.png"ggsave(file=two_plot_name,width=15,height=8,two_plots)The next set of code repeats the standard error plot for the annual change in the employment timeseries.
#now do the annual change plotlfs_change_annual<-diff(canada_lfs_ts[,1],differences=1,lag=12)#the data have to be merged together to maintain the ts attributesdata12<-cbind(canada_lfs_ts[,1],lfs_change_annual,canada_lfs_ts[,5])colnames(data12)<-c("LFS15+","DeltaLFS15+12","SEDeltalfs15+12")tail(data12,12)plot_data<-cbind(data12[,2],data12[,2]+.5*data12[,3],data12[,2]-.5*data12[,3])colnames(plot_data)<-c("DeltaLFS15A","Upper","Lower")numb_obs<-nrow(plot_data)plot_data2<-spread(ts_tbl(subset(plot_data,start=numb_obs-23)),id,value) #go for a wide tibble to make the chart easier#now calculate a date string for the captiondate_string<-paste0(substr(plot_data2$time[1],1,7),"/",substr(tail(plot_data2$time,1),1,7))head(plot_data2)#load the plot librarylibrary(ggplot2)plot12<-ggplot(plot_data2,aes(x=time,y=DeltaLFS15A))+geom_point()+geom_pointrange(aes(ymin=Lower,ymax=Upper))+geom_line()+labs(title="Annual Change in LFS 15+ Employment",y="Annual Change (000)",x=NULL,subtitle="Seasonally Adjusted with Standard Error Bars",caption=paste(date_string," ","STATCAN:",paste(canada_lfs_vbls[c(1,5)],collapse=", "),"JCI"))ggsave(plot12,file="LFS15_annual_change.png")plot_list<-mget(c("plot1","plot12"))two_plots<-marrangeGrob(plot_list,nrow=1,ncol=2,top=NULL)two_plot_name<-"lfs_se_monthly_annual.png"ggsave(file=two_plot_name,width=15,height=8,two_plots)Now we start the actual seasonal adjustment examples using stl as the first one.
#now start some seasonal adjustment tests#the raw series is the 6th and last in the list of requested vectorsstc_sa<-canada_lfs_ts[,1]stc_raw<-canada_lfs_ts[,6]#first we will use the stl packageempl_stl_fit<-mstl(stc_raw,robust=TRUE)print(summary(empl_stl_fit))stl_output<-capture.output(summary(empl_stl_fit))#now write it outcat("stl Results",stl_output,file="LFS15_stl_components_analysis.txt",sep="\n")empl_stl_sa<-seasadj(empl_stl_fit)stl_component_plot<-autoplot(empl_stl_fit)+labs(title="Total Employment Decomposition LFS15+",subtitle="Decomposition using STL - LOESS (000)",caption=paste("STATCAN:",canada_lfs_vbls[6],"JCI"))ggsave(stl_component_plot,file="LFS15_stl_components.png")In the code above, the mstl procedure from the forecast package is used rather than the stl version in the base R implementation. The mstl approach provides a slightly tighter fit by iterating the stl process. All of the seasonal adjustment procedures produce some object which can be displayed with the summary function. The capture.output function is used to capture the summary results to a text variable which is written out to a text file. This text file was inserted into the seasonal adjustment report. The autoplot function from the forecast package extends the standard ggplot2 library to facilitate the plotting of timeseries and related objects. For the mstl/stl procedure, the resulting object (empl_stl_fit) includes all of the decomposition components. The seasadj function is used to extract the seasonally-adjusted timeseries.
The next stage uses the seas function from the seasonal package from Sax to access the Bureau of the Census binaries to do the X13-SEATS analysis,
#now we are going to try x-13library(seasonal)empl_x13_fit<-seas(stc_raw)empl_x13_sa<-final(empl_x13_fit)print(summary(empl_x13_fit))x13_component_plot<-autoplot(empl_x13_fit)+labs(title="Total Employment Decomposition LFS15+",subtitle="Decomposition using X13 -default settings (000)",caption=paste("STATCAN:",canada_lfs_vbls[6],"JCI"))ggsave(x13_component_plot,file="LFS15_x13_components.png")#now lets save the x13 results as a text filex13_output<-capture.output(summary(empl_x13_fit))#now write it outcat("X13 Results",x13_output,file="LFS15_x13_components_analysis.txt",sep="\n")In this case, the final function extracts the seasonally-adjusted series.
The next code segment repeats the same process but sets the x11 option to a null string to get the base X11 Arima analysis.
#now we will do the x11-variantempl_x11_fit<-seas(stc_raw,x11="")empl_x11_sa<-final(empl_x11_fit)print(summary(empl_x11_fit))x11_component_plot<-autoplot(empl_x11_fit)+labs(title="Total Employment Decomposition LFS15+",subtitle="Decomposition using x11 -default settings (000)",caption=paste("STATCAN:",canada_lfs_vbls[6],"JCI"))ggsave(x11_component_plot,file="LFS15_x11_components.png")#now lets save the x11 results as a text filex11_output<-capture.output(summary(empl_x11_fit))#now write it outcat("x11 Results",x11_output,file="LFS15_x11_components_analysis.txt",sep="\n")The next section of code plots the seasonally-adjusted time series over the whole range processed and over a shorter range.
#comparison of three methodsplot_data3<-cbind(stc_sa,empl_stl_sa,empl_x13_sa,empl_x11_sa)colnames(plot_data3)<-c("STATCAN","MSTL-LOESS","X13-SEATS","X-11")plot_tibble<-ts_tbl(plot_data3)last_date<-substr(max(plot_tibble$time),1,7)stc_text<-paste("STATCAN: raw:",canada_lfs_vbls[6],"SA:",canada_lfs_vbls[1],"as of ",last_date,"JCI")sa_plot<-ggplot(plot_tibble,aes(x=time,y=value,colour=id,group=id))+geom_line(aes(linetype=id))+theme(axis.title.x=element_blank(),legend.title=element_blank(),legend.position="bottom")+labs(title="Comparison of Seasonally Adjusted LFS15+ Employment",subtitle="Methods are STL-LOESS, X11, X13-SEATS and STATCAN-X12",y="Employment (000)",caption=stc_text)ggsave(sa_plot,file="LFS15_sa_alternatives_full.png")#shorter time horizaonplot_data4<-window(plot_data3,start=2016)plot_tibble<-ts_tbl(plot_data4)last_date<-substr(max(plot_tibble$time),1,7)stc_text<-paste("STATCAN: raw:",canada_lfs_vbls[6],"SA:",canada_lfs_vbls[1],"as of ",last_date,"JCI")sa_plot4<-ggplot(plot_tibble,aes(x=time,y=value,colour=id,group=id))+geom_line(aes(linetype=id))+theme(axis.title.x=element_blank(),legend.title=element_blank(),legend.position="bottom")+labs(title="Comparison of Seasonally Adjusted LFS15+ Employment",subtitle="Methods are STL-LOESS,X13-SEATS and STATCAN-X12",y="Employment (000)",caption=stc_text)ggsave(sa_plot4,file="LFS15_sa_alternatives_short.png")The next set of code plots the irregular, trend-cycle and seasonal components using facets so that they are compared on a common scale for each component.
#add a comparison of irregularsstl_irregular<-remainder(empl_stl_fit)x11_irregular<-irregular(empl_x11_fit)x13_irregular<-irregular(empl_x13_fit)plot_data_5<-cbind(stl_irregular,x11_irregular,x13_irregular)plot_tibble<-ts_tbl(plot_data_5)irr_plot<-ggplot(plot_tibble,aes(x=time,y=value,colour=id,group=id,fill=id,facet=id))+theme(axis.title.x=element_blank(),legend.title=element_blank(),legend.position="bottom")+labs(title="Comparison of Seasonal Adjustment Residuals LFS15+ Employment",subtitle="Methods are STL-LOESS, X11, X13-SEATS",y="Employment (000)",caption=stc_text)+geom_col()+facet_wrap(~id,ncol=1)ggsave(irr_plot,file="LFS15_sa_irregular.png")#add a comparison of trendcyclesstl_trendcycle<-trendcycle(empl_stl_fit)x11_trendcycle<-trend(empl_x11_fit)x13_trendcycle<-trend(empl_x13_fit)plot_data_5<-cbind(stl_trendcycle,x11_trendcycle,x13_trendcycle)plot_tibble<-ts_tbl(plot_data_5)trend_plot<-ggplot(plot_tibble,aes(x=time,y=value,colour=id,group=id,fill=id,facet=id))+theme(axis.title.x=element_blank(),legend.title=element_blank(),legend.position="bottom")+labs(title="Comparison of Seasonal Adjustment Trendcycle LFS15+ Employment",subtitle="Methods are STL-LOESS, X11, X13-SEATS",y="Employment (000)",caption=stc_text)+geom_line(aes(linetype=id))+facet_wrap(~id,ncol=1)ggsave(trend_plot,file="LFS15_sa_trendcycle.png")plot_tibble<-ts_tbl(plot_data_5)trend_plot<-ggplot(plot_tibble,aes(x=time,y=value,colour=id,group=id,fill=id))+theme(axis.title.x=element_blank(),legend.title=element_blank(),legend.position="bottom")+labs(title="Comparison of Seasonal Adjustment Trendcycle LFS15+ Employment",subtitle="Methods are STL-LOESS, X11, X13-SEATS",y="Employment (000)",caption=stc_text)+geom_line(aes(linetype=id))ggsave(trend_plot,file="LFS15_sa_trendcycle_oneplot.png")#add a comparison of seasonals#the seasonals must be extracted from the object result from seasstl_seasonal<-seasonal(empl_stl_fit)x11_seasonal<-(empl_x11_fit$data[,"seasonal"])x13_seasonal<-(empl_x13_fit$data[,"seasonal"])plot_data_6<-cbind(stl_seasonal,x11_seasonal,x13_seasonal)plot_tibble<-ts_tbl(plot_data_6)seasonal_plot<-ggplot(plot_tibble,aes(x=time,y=value,colour=id,group=id,fill=id,facet=id))+theme(axis.title.x=element_blank(),legend.title=element_blank(),legend.position="bottom")+labs(title="Comparison of Seasonal Adjustment Seasonals LFS15+ Employment",subtitle="Methods are STL-LOESS, X11, X13-SEATS",y="Employment (000)",caption=stc_text)+geom_line(aes(linetype=id))+facet_wrap(~id,ncol=1)ggsave(seasonal_plot,file="LFS15_sa_seasonal.png")There are functions to extract the three components for stl but not for the seas function. The latter package includes functions for the first two components only. Therefore, the seasonal portion must be extracted directly from the fit object returned by the seas function.
The next set of code uses the summary function to analyze the set of components.
#compare the seasonalsd1<-cbind(stl_seasonal,x11_seasonal,x13_seasonal)summary(d1)#sappply can be used to apply a function to each column of a data frame#alternatively use one of the map functions from purrr for more flexibilitysapply(d1,sd,na.rm=TRUE)d2<-cbind(stl_trendcycle,x11_trendcycle,x13_trendcycle)summary(d2)sapply(d2,sd,na.rm=TRUE)d3<-cbind(stl_irregular,x11_irregular,x13_irregular)summary(d3)sapply(d3,sd,na.rm=TRUE)The sapply procedure is used to apply the standard deviation (“sd”) procedure separately to each column in the data frame. If you use apply “sd” to the frame, all 3 columns are combined which is not useful.
The results are not very nicely formatted so the final set of code uses the stargazer package to produce a formatted HTML table of statistics. This is written out to an HTML file.
library(stargazer)#prepare a sett of summaries with stargazerd_components<-cbind(stl_seasonal,x11_seasonal,x13_seasonal,stl_trendcycle,x11_trendcycle,x13_trendcycle,stl_irregular,x11_irregular,x13_irregular)stargazer(d_components,summary=TRUE,type="html",out="statistics_components.html")d_sa<-cbind(empl_stl_sa,empl_x11_sa,empl_x13_sa,stc_sa)stargazer(d_sa,summary=TRUE,type="html",out="statistics_sa.html")d_sa_2010<-window(d_sa,start=2010)stargazer(d_sa_2010,summary=TRUE,type="html",out="statistics_sa_2010.html")If the output html files are opened in a web browser, the material can be copied and pasted to a report. There are other packages for doing nicely formatted summaries, but stargazer is useful for reporting regression results and other data. It can also produce LaTex and ascii. The package echoes its HTML output to the console.
[1] This note has benefited from advice and criticism from Dr. Philip Smith. All responsibility for the errors, omissions and opinions rests with the author Paul Jacobson.
[2] The examples were run using Statistics Canada’s data retrieved as of January 28, 2019.
[3] https://www.rdocumentation.org/packages/seasonal/versions/1.7.0
[4] https://www.rdocumentation.org/packages/stats/versions/3.5.2/topics/stl
[5] https://otexts.com/fpp2/stl.html
[6] Alexander Cairncross. (n.d.). AZQuotes.com. Retrieved January 23, 2019, from AZQuotes.com Web site: https://www.azquotes.com/quote/757581
Analyzing Financial Indicators By Country From The OECD With R
In this example, we will use the OECD package to access financial indicators data by country. Because it is a different dataset, the approach must be completely adjusted for differences in nomenclature and organization.
Packages USED
The key package used in this vignette is the oecd package which accesses stats database from the OECD.[1] Key packages include
- dplyr – for processing the tibble
- ggplot2 – part of tidyverse for plotting the results
- OECD – package to access data using OECD stats api.[2]
Examing the Data Structure
The initial stage is to search for available databases.
#OECD RUNlibrary(OECD)library(tidyverse)library(gdata)#get data set listdataset_list <- get_datasets()search_results<-search_dataset("Financial Indicators", data = dataset_list)print(search_results)#data_set<-"FIN_IND_FBS"search_results %>%filter(id==data_set)%>%select(title)->data_set_titletypeof(data_set_title)data_set_title<-as.character(unlist(data_set_title))print(data_set_title)dstruct<-get_data_structure(data_set)str(dstruct,max.level=1)dstruct$VAR_DESC # id description# 1 LOCATION Country# 2 INDICATOR Indicator# 3 TIME Time# 4 OBS_VALUE Observation Value# 5 TIME_FORMAT Time Format# 6 OBS_STATUS Observation Status# 7 UNIT Unit# 8 POWERCODE Unit multiplier# 9 REFERENCEPERIOD Reference periodprint(dstruct$INDICATOR)The code above shows how to inspect the structure of a given data set. In this case, we are looking at the “Financial Indicators – Stocks”. Each dataset in OECD.stat (https://stats.oecd.org) has a different structure. Target databases can be evaluated using the stats.oecd.org web site.
There are a large number of indicators. By inspection, we have chosen:
- Debt of general government, as a percentage of GDP
- Debt of households and NPISHs, as a percentage of GDI
- Private sector debt, as a percentage of GDP
- Total net worth of households and NPISHs, as a percentage of GDI
Retrieving the data
indicator_table<-dstruct$INDICATOR[c(13,15,18,20),]print(indicator_table)indicator_vector<-unlist(indicator_table["id"])indicator_title<-unlist(indicator_table["label"])#define the countries we are going to charttarget_locations<-c("CAN","USA","FRA","DEU","GBR","DNK","NLD","NZL","AUS","NOR","ESP")filter_list<-list(target_locations,indicator_vector)data1<-get_dataset(dataset=data_set,filter=filter_list)Filters have to be set in the order of variables shown in the variable description above to reduce the data retrieval to manageable proportions. The retrieved dataset is saved as an XLSX file in the default directory to provide a snapshot of data. This is often a requirement when delivering research because data gets revised. The advantage of the XLSX data structure is it is now an open data standard. The openxlsx package creates the file without using any Microsoft or Java libraries. If one wanted only to postprocess the data in R, it would be better to save the data1 tibble using saveRDS, a native R command which saves in a compact binary form. The command readRDS could be used to read the file in,
ibrary(openxlsx)write.xlsx(data1,file=paste0("OECD_Financial_indicators",Sys.Date(),".xlsx"))Process and Plot the Data by Indicator
The next set of code is the key processing loop which processes the data1 object by indicator and does 4 plots.
or(this_chart in seq_along(indicator_vector)){ # print(this_chart) this_indicator<-indicator_vector[this_chart] this_title<-indicator_title[this_chart] title_sections<-unlist(strsplit(this_title,",",fixed=TRUE)) print(this_title) plot_data<-data1 %>% filter(INDICATOR==this_indicator)%>% group_by(LOCATION) %>% arrange(obsTime) %>% slice(n()) %>% ungroup() # print(as.data.frame(plot_data)) max_obs_value<-max(plot_data$obsValue) cat("maximum is ",max_obs_value,"\n") text_adjust_factor<-.1*max(abs((plot_data$obsValue))) target_title="Percentage" plot1<-ggplot(plot_data,aes(x=LOCATION,y=obsValue, label=paste(round(obsValue,1),"-",obsTime)))+ labs(y=target_title,x=NULL, title=title_sections[1], subtitle=title_sections[2], caption=paste("OECD:",data_set_title,"JCI",Sys.Date()))+ geom_bar(stat="identity",fill="light green")+ theme(plot.title=element_text(size=12), plot.subtitle=element_text(size=10),plot.caption=element_text(size=7))+ geom_text(size=2.5,angle=90,aes(y=(sign(obsValue)* # (text_adjust_factor+abs(obsValue))))) (1.2*abs(obsValue))))) ggsave(plot1,file=paste0(this_indicator,".png"),width=8,height=10.5) #rename the plots mv(from="plot1",to=paste0(this_indicator,"_plot1"))}The plot data is constructed by filtering by indicator and then grouping by location, sorting by time and extracting via the slice operator only the last observation. The title is split into two sections to provide a more readable title and subtitle. This code is naturally dependent on the specific title structure of the indicator. In the plot, labels are constructed from the year and value being plotted.
In this deck, we are not using facets, we are going to manage each plot independently. However, the ggplot function returns the same object each time through the loop. Therefore, at the bottom of the loop, the MV command from the gdata package is used to move the plot1 object to a named object which is constructed from the indicator name.
Grouping the Plots
In this example, the named plots are grouped using gridExtra’s functions to provide the example shown below.
library(gridExtra)plot_names<-paste0(indicator_vector,"_plot1")plot_list<-mget(plot_names)multi_plots<-marrangeGrob(plot_list,ncol=2,nrow=2,top=NULL)multi_plot_name<-"Debt_summary.png"ggsave(file=multi_plot_name,width=8,height=10.5,multi_plots)
Analyzing Health Expenditure Data By Country From The OECD With R
In this example, we will use the OECD package to access health expenditure data by country.
Packages USED
The key package used in this vignette is the oecd package which accesses stats database from the OECD.[1] Key packages include
- dplyr – for processing the tibble prior to conversion to xts
- ggplot2 – part of tidyverse for plotting the results
- OECD – package to access data using OECD stats api.[2]
Examing the Data Structure
The initial stage is to search for available health related databases.
#OECD RUNLibrary(OECD)library(dplyr)library(ggplot2)#define the countries we are going to charttarget_locations<-c("CAN","USA","FRA","DEU","GBR","DNK","NLD","NZL","AUS","NOR","ESP")#get data set listdataset_list <- get_datasets()p1<-search_dataset("health", data = dataset_list)#we will use SHA which is the 6th in the result p1data_set<-as.character(p1$id[6])data_set_title<-as.character(p1$title[6])#now we will get the structure of the datasetdstruct<-get_data_structure(data_set)str(dstruct,max.level=1)print(dstruct$VAR_DESC)#now examine the structure - the first sections are key # id description# 1 HF Financing scheme# 2 HC Function# 3 HP Provider# 4 MEASURE Measure# 5 LOCATION Countryprint(dstruct$HF)print(dstruct$HC)print(dstruct$HP)print(dstruct$MEASURE)The code above shows how to inspect the structure of a given data set. Each dataset in OECD.stat (https://stats.oecd.org) has a different structure. Target databases can be evaluated using the stats.oecd.org web site. The order of the variables in the VAR_DESC table reflects their hierarchy in the dataset. HF specifically addresses total funding, funding by government or insurance scheme etc.
id label1 HFTOT All financing schemes2 HF1 Government/compulsory schemes3 HF11 Government schemes4 HF12HF13 Compulsory contributory health insurance schemes5 HF121 Social health insurance schemes6 HF122 Compulsory private insurance schemes7 HF2HF3 Voluntary schemes/household out-of-pocket payments8 HF2 Voluntary health care payment schemes9 HF21 Voluntary health insurance schemes10 HF22 NPISH financing schemes11 HF23 Enterprise financing schemes12 HF3 Household out-of-pocket payments13 HF31 Out-of-pocket excluding cost-sharing14 HF32 Cost-sharing with third-party payers15 HF4 Rest of the world financing schemes (non-resident)16 HF42 Voluntary schemes (non-resident)17 HF0 Financing schemes unknownRetrieving the data
The top level of financing will be used with the exception of financing from non-residents for this analysis. For this analysis, we will focus on aggregate health expenditure (HCTOT) and services provided by all providers (HPTOT). The code has been developed to cycle through a list of measures. In this case, we will use PARPIB, the GDP share, and PPPPER, expenditure per capita on a purchasing power parity basis.
function_target="HCTOT"unction_title=filter(dstruct$HC,id==function_target)%>%select(label)target_financing<-c("HFTOT","HF1","HF2","HF3")filter_list<-list(target_financing,function_target,"HPTOT")data1<-get_dataset(dataset=data_set,filter=filter_list)#save base dataset as an excel file for documentationlibrary(openxlsx)write.xlsx(data1,file=paste0("SHA_financing_",Sys.Date(),".xlsx"))#Filters have to be set in the order of variables to reduce the data retrieval to manageable proportions. The retrieved dataset is saved as an XLSX file in the default directory to provide a snapshot of data. This is often a requirement when delivering research because data gets revised. The advantage of the XLSX data structure is it is now an open data standard. The openxlsx package creates the file without using any Microsoft or Java libraries. If one wanted only to postprocess the data in R, it would be better to save the data1 tibble using saveRDS, a native R command which saves in a compact binary form. The command readRDS could be used to read the file in,
Process and Plot the Data by Measure
The next set of code sets up filters to be used by dplyr to further process the retrieved data. A location list is prepared using standard 3 character country codes which are common across many international data providers. The selected locations are defined in the character vector target_locations at the top of the script.
#now we will parse by locations and the measure - share of gdplocation_table<-dstruct$LOCATIONlocation_factor<-factor(target_locations,levels=target_locations)location_titles<-filter(dstruct$LOCATION,id %in% target_locations) %>%select(label)#define the measure to be used# target_measure<-"PARPIB"target_measure<-"PPPPER"measures_list<-c("PARPIB","PPPPER")for(target_measure in measures_list){ target_title<-filter(dstruct$MEASURE,id==target_measure) %>% select(label)%>% as.character() #define financing labels financing_labels<-filter(dstruct$HF,id %in% target_financing) %>% select(label) #organize data #the left_joins add labels for location and financing (label.x label.y) data2<-data1 %>% filter(LOCATION %in% target_locations,MEASURE==target_measure) %>% select(HF,LOCATION,obsValue,obsTime) %>% group_by(HF,LOCATION)%>% arrange(obsTime) %>% slice(n()) %>%ungroup()%>% left_join(location_table,by=c("LOCATION"="id")) %>% left_join(dstruct$HF,by=c("HF"="id"))The loops over the list of measures in this version of the code. The data2 table is created from the initial retrieval. Only the last observation (ragged) is retained by using the slice function. The name of the country and the financing title are joined with left_joins. At this juncture, the country name is not actually used.
Because there are varying terminal years, the year, in the variable obsTime, is appended to the value to label the datapoint. In the plot, the label.y variable, the label from the financing table, is used as a grouping table so that the plots are separated by financing. As much as possible, the plot uses title information obtained from the database.
data_year<-unique(data2$obsTime) print(data_year) #start plot #text adjustment factor to move the point labels high enough text_adjust_factor<-.125*max(data2$obsValue) plot1<-ggplot(data2,aes(x=LOCATION,y=obsValue,group=label.y, label=paste(round(obsValue,1),"-",obsTime)))+ labs(y=target_title,x=NULL, title=function_title,caption=paste("OECD:",data_set_title,"JCI"))+ geom_bar(stat="identity",fill="light green")+ geom_text(size=2.5,angle=90,aes(y=(sign(obsValue)* (text_adjust_factor+abs(obsValue)))))+ facet_wrap(~label.y,ncol=2)ggsave(plot1,file=paste0(function_title,"_",function_target,"_",target_measure,".png"),width=8,height=10.5)}The plot is saved as 4 facets (small sub plots) using facet_wrap function which references the lable.y financing title. A text adjustment factor is calculated to move the value and year labels high enough above the bars. A file name to save the plot is developed.
The example plots are shown below.


